Wprowadzenie do metod Monte Carlo

Metody Monte Carlo polegają na wykorzystaniu losowości w celu rozwiązywania problemów, które mogą być deterministyczne w ujęciu teoretycznym. Metoda polega na wielokrotnym próbkowaniu z określonej przestrzeni i wykorzystaniu wyników próbek do przybliżenia rozwiązania.

Monte Carlo – teoria

Załóżmy, że chcemy obliczyć wartość całki oznaczonej funkcji $f(x)$ w przedziale $[a, b]$, tzn.:

$$ I = \int_a^b f(x) dx $$

Całkowanie metodą Monte Carlo opiera się na przybliżeniu wartości tej całki przez uśrednienie wartości funkcji $f(x)$ dla losowo wybranych punktów w przedziale $[a, b]$. Musimy zatem wykonać następujące kroki:

1. Wybieramy $N$ losowych punktów $x_1, x_2, …, x_N$ w przedziale $[a, b]$.
2. Obliczamy średnią wartość funkcji:
   $$ \mu = \frac{1}{N} \sum_{i=1}^N f(x_i) $$
3. Mnożymy tę średnią przez długość przedziału $(b-a)$, aby uzyskać przybliżoną wartości całki:
   $$ I  \approx (b-a) \times \mu = \frac{b-a}{N} \sum_{i=1}^N f(x_i)  $$

Metoda ta jest oparta na prawie wielkich liczb, które mówi, że jeśli mamy ciąg niezależnych zmiennych losowych $X_1, X_2, …, X_N$ o tej samej wartości oczekiwanej $\mu$ i skończonej wariancji $\sigma^2 < \infty$, to dla $N$ dążącego do nieskończoności średnia z tych zmiennych dąży do wartości oczekiwanej:

$$ \frac{1}{N} \sum_{i=1}^N X_i \rightarrow \mu \ \text{dla} \ N \rightarrow \infty $$

W praktyce, liczba próbek $N$ nie jest nieskończona, ale im większa jest wartość $N$, tym dokładniejsze jest przybliżenie. Metoda Monte Carlo jest szczególnie przydatna, gdy nie jesteśmy w stanie łatwo znaleźć rozwiązania za pomocą standardowych metod analitycznych.

Monte Carlo – praktyka

Przybliżanie wartości $\pi$

Jednym z klasycznych zastosowań metod Monte Carlo jest przybliżenie wartości liczby $\pi$. Załóżmy, że mamy kwadrat o boku długości $1$ i koło wpisane w ten kwadrat. Pole powierzchni koła o promieniu $r$ wynosi $A = \pi r^2$, a pole powierzchni kwadratu o boku $b$ wynosi $B = b^2$. Jeśli promień wynosi $r = \frac{1}{2}$, to bok kwadratu, w który wpisane jest to koło wynosi $b = 2r = 1$.  Wówczas stosunek pola powierzchni koła do pola powierzchni kwadratu wynosi:

$$\frac{A}{B} =  \frac{\pi (\frac{1}{2})^2}{1^2} = \frac{\pi}{4}$$

zatem wartość $\pi$ wynosi:

$$ \pi = 4 \times \frac{A}{B} $$

Aby zastosować metodę Monte Carlo do przybliżenia wartości $\pi$ musimy wykonać następujące kroki:

1. Ustalamy rozmiar próbki $N$.
2. Losujemy $2N$ punktów z rozkładu jednostajnego na odcinku $[-0.5, 0.5]$. Wylosowane punkty będą odpowiadać punktom na płaszyźnie o współrzędnych $(x_i, y_i)$ dla $i = 1, \dots, N$. Odcinek $[-0.5, 0.5]$ został wybrany tak, aby promień koła wynosił $r=0.5$, natomiast bok kwadratu wynosił $b=1$.
3. Zauważmy, że wszystkie wylosowane punkty leżą wewnątrz kwadratu. Zatem musimy policzyć ile z tych punktów leży wewnątrz koła, czyli ile punktów $(x, y)$ spełnia następującą  nierówność:
   $$ x^2 + y^2 \leq \left( \frac{1}{2} \right)^2$$
4. Oznaczmy ilość punktów spełniających powyższą nierówność jako $M$. Wówczas możemy oszacować wartość $\pi$ jako:
   $$ \pi \approx 4 \times \frac{M}{N} $$

Implementacja w RStudio

Poniżej widzimy implementację powyższej procedury w języku R.

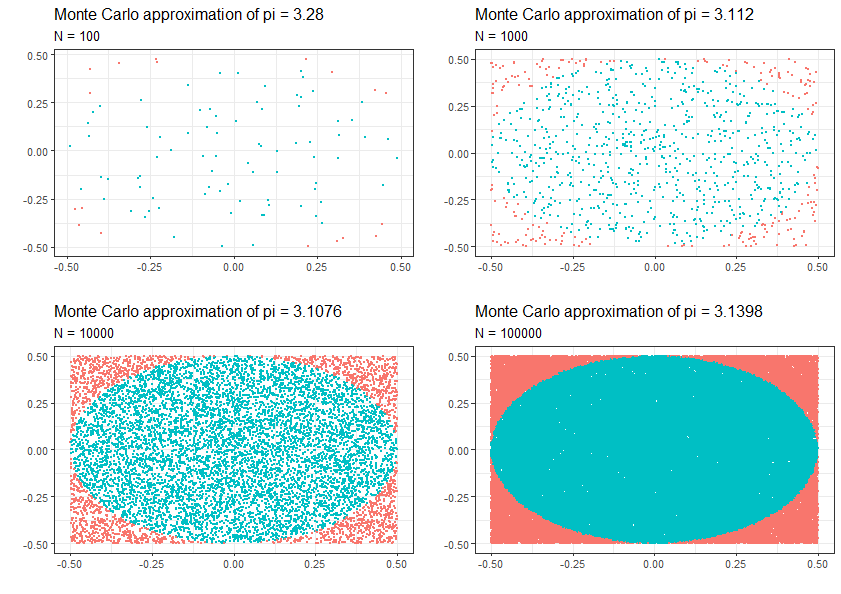
Wykonajmy tę procedurę dla $N = 100, 1000, 10000, 100000$. Widzimy, że im wyższa wartość $N$ tym dokładniejsze przybliżenie liczby $\pi$. Kolorem irysowo-niebieskim zaznaczono punkty leżące wewnątrz koła, natomiast kolorem czerwonym zaznaczono kolory leżące wewnątrz kwadratu ale leżące poza kołem.

Inne zastosowania metod Monte Carlo można znaleźć w artykułach na naszej stronie:

• Optymalizacja portfela inwestycyjnego metodami Monte Carlo

Pełny kod R można znaleźć na Github.