Wartość zagrożona ryzykiem – RStudio

Koncepcja wartości zagrożonej ryzykiem (VaR, ang. Value at Risk) została opracowana w latach dziewięćdziesiątych przez analityków z banku J.P. Morgan. Celem VaR jest określenie najgorszej możliwej straty, która może wystąpić z danym poziomem ufności, na przykład 95% lub 99%. W praktyce jest to jedna z najczęściej stosowanych miar ryzyka.

Wprowadzenie do VaR

Załóżmy, że mamy portfel inwestycyjny i chcemy ocenić ryzyko związane z tą inwestycją. VaR pomaga nam zrozumieć, jak dużą stratę możemy ponieść w najgorszym scenariuszu. Wyraża się to za pomocą kwoty pieniężnej lub procentu wartości portfela.

Formalnie, dla poziomu ufności $(1-\alpha)$, wartość zagrożona ryzykiem $VaR_{\alpha}$ to kwota, którą nie przekroczy strata portfela z prawdopodobieństwem $(1-\alpha)$:

$$ \mathbb{P} \left( L >  VaR_{\alpha} \right) = \alpha$$

gdzie $L$ to strata portfela.

Metody estymacji VaR

Istnieje wiele metod do estymacji VaR, niektóre z nich to:

1. Metoda historyczna: Jest to najprostsza metoda, która polega na bezpośrednim oszacowaniu VaR na podstawie danych historycznych.
2. Metody parametryczne: Te metody zakładają, że dane mają konkretny rozkład prawdopodobieństwa, na przykład rozkład normalny lub rozkład t-Studenta.
3. Metody symulacyjne: Te metody polegają na generowaniu danych za pomocą symulacji Monte Carlo.
4. Model EWMA (Exponentially Weighted Moving Average): Jest to model, który zakłada, że ostatnie obserwacje mają większy wpływ na szacowaną wartość wariancji, a wpływ starszych obserwacji maleje wykładniczo.
5. Model GARCH (Generalized Autoregressive Conditional Heteroskedasticity): Jest to model, który zakłada, że wariancja zwrotów jest warunkowa i zależy od własnych przeszłych wartości.

Implementacja w R

Wczytujemy dane ze zbioru EuStockMarkets, który zawiera ceny zamknięcia dla 4 europejskich indeksów giełdowych za okres 1991-1998. Liczymy logarytmiczne stopy zwrotu, dla których będziemy szacować VaR.

Ustalamy poziom istotności $\alpha = 5\%$.

Metoda historyczna

W tej metodzie VaR to po prostu $\alpha$-kwantyl historycznych stóp zwotu.

W powyższym przykładzie otrzymaliśmy wynik -0.0158. Oznacza to, że według metody historycznej istnieje 5% prawdopodobieństwo, że dzienna strata przekroczy 1.58%. Innymi słowy, inwestując 10000 złotych w ten indeks, mamy 95% prawdopodobieństwo, że dzienne obsunięcie kapitału nie przekroczy 158 zł.

Metoda parametryczna

W metodzie parametrycznej najpierw estymujemy parametry rozkładu bazując na danych historycznych. W przypadku rozkładu normalnego będzie to średnia oraz wariancja. Następnie używamy tych parametrów do obliczenia kwantyli rozkładu.

Rozkład t-Studenta jest często stosowany w analizie ryzyka finansowego, ponieważ lepiej od rozkładu normalnego opisuje grube ogony rozkładów, czyli zdarzenia ekstremalne. Najpierw musimy znormalizować stopy zwrotu, a następnie dopasować ilość stopni swobody, ponieważ parametr ten decyduje o grubości ogonów rozkładu. Im mniejsza wartość df, tym grubsze są ogony, co oznacza większe prawdopodobieństwo wystąpienia skrajnych wartości. Dopiero wtedy możemy obliczyć VaR jako kwantyl rozkładu t-Studenta, pamiętając o denormalizacji, czyli:

$$VaR_{\alpha}^t =  \mu + \sigma \cdot t_{\alpha , \ df}$$

Metody symulacyjne

W metodzie symulacyjnej najpierw generujemy symulowane zwroty z odpowiedniego rozkładu prawdopodobieństwa. Następnie obliczamy VaR jako kwantyl wygenerowaje próbki. W poniższym przykładzie generujemy próbkę wielkości 10000 z rozkładu t-Studenta.

Model EWMA

Model EWMA zakłada, że wariancja jest ważona wykładniczo. To podejście jest często używane w analizie finansowej, ponieważ uznaje się, że najnowsze dane są najbardziej informacyjne. Parametr $\lambda$ kontroluje szybkość, z jaką wpływ starszych obserwacji maleje. Najczęściej stosuje się wartości parametru $\lambda$ od $0.94$ do $0.98$. W modelu EWMA wariancję obliczamy następująco:

$$ \sigma^2_{t+1} = \lambda \sigma_t^2 + \left( 1 – \lambda \right) r_t^2 $$

gdzie $r_t$ to stopa zwrotu zwrot w chwili $t$, a $\sigma_t^2$ to wariancja w chwili $t$.

Liczymy VaR mnożąc kwantyl odpowiedniego rozkładu przez ostatnią wartość wektora wariancji oszacowanego za pomocą modelu EWMA. W tym kontekście, VaR mierzy maksymalną strate, której możemy się spodziewać na następny dzień z danym poziomem ufności. Jest to zgodne z podstawowym założeniem modeli EWMA,  że najnowsze dane są najbardziej informacyjne dla przewidywania przyszłej zmienności.

Model GARCH

W modelu GARCH najpierw dokonujemy specyfikacji odpowiedniego modelu, a następnie dopasowujemy go do naszych danych. VaR jest obliczane na podstawie oszacowanej wariancji, podobnie jak obliczaliśmy to w modelu EWMA.

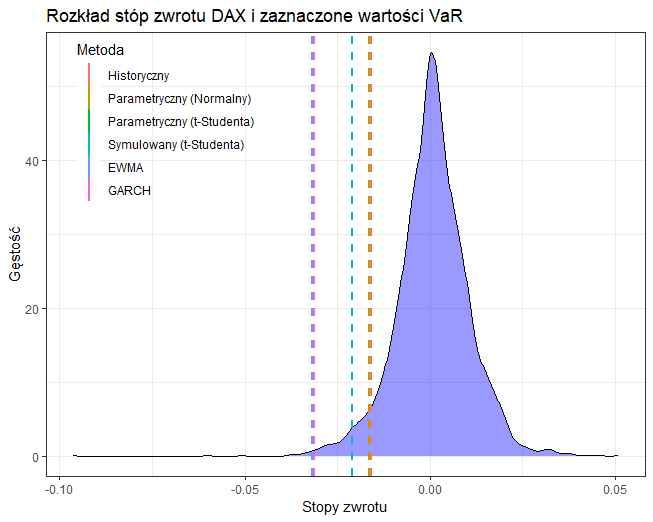
Porównanie wyników

Poniżej widzimy wizualizację wyników wykonaną za pomocą biblioteki ggplot2. Metoda historyczna oraz metoda zakładająca rozkład normalny zdają się niedoszacowywać potencjalnego ryzyka. Metoda zakładająca rozkład t-Studenta, zarówno parametryczna jak i symulacyjna dały bardzo zbliżony wynik, trochę wyższy od dwóch poprzednich metod. Największe ryzyko przewidują metody oparte na EWMA oraz GARCH, które z założenia przypisują większą wagę najświeższym informacjom.

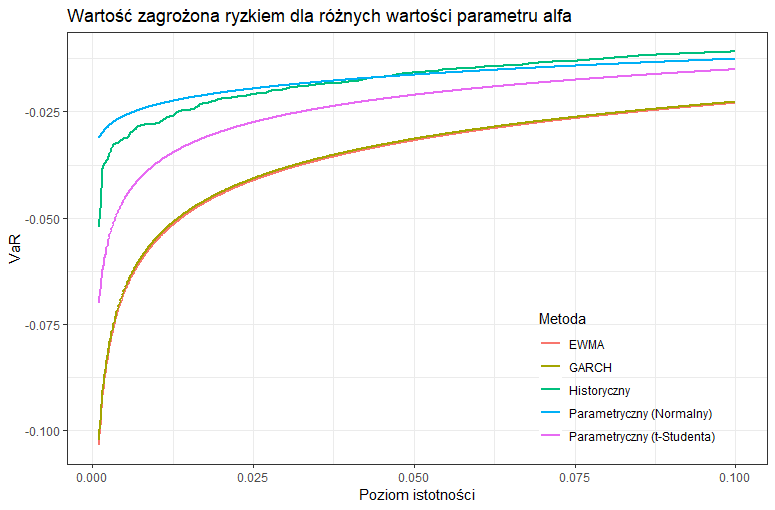
VaR dla różnych wartości parametru $\alpha$

Poniżej widzimy wartość zagrożoną ryzykiem dla wartości parametru $\alpha$ od $0.1\%$ do $10%$. Możemy zauważyć, że im większy poziom istotności $\alpha$, tym mniejsze szacowane ryzyko.

Pełny kod R można znaleźć na Github.