Value-at-Risk oraz metody Monte Carlo w optymalizacji portfela
W jednym z artykułów na naszej stronie opisaliśmy zastosowanie symulacji Monte Carlo do wyboru optymalnego portfela. Wówczas kryterium optymalizacyjnym była minimalizacja zmienności mierzonej odchyleniem standardowym oraz maksymalizacja współczynnika Sharpe’a który określa stosunek zysku do ryzyka. W tym artykule zastosujemy tę samą procedurę, ale jako miarę ryzyka zamiast odchylenia standardowego przyjmiemy wartość zagrożoną ryzykiem (ang. Value-at-Risk) oraz warunkową wartość zagrożoną ryzykiem (ang. Expected Shortfall).
Czym jest Value-at-Risk?
Wartość zagrożoną ryzykiem definiujemy jako maksymalną wartość straty, jaką portfel inwestycyjny może ponieść w określonym horyzoncie czasowym z określonym poziomem istotności (najczęściej jest to 5% lub 1%). Formalnie możemy to zapisać jako:
$$ \mathbb{P} \left( L > VaR_{\alpha} \right) = \alpha \text{,} $$
gdzie $L$ to strata portfela. W tym artykule zastosujemy tzw. metodę historyczną do oszacowania wartości zagrożonej ryzykiem. W tej metodzie wyznaczamy po prostu $\alpha$-kwantyl historycznych stóp zwrotu portfela. Jest to najprostsza metoda, aczkolwiek najbardziej podatna na niedoszacowania lub na przeszacowania. Na naszej stronie internetowej możecie przeczytać artykuł na temat szacowania Value-at-Risk kilkoma różnymi metodami.
Jednak miara Value-at-Risk mówi nam jedynie jaką wartość może przekroczyć potencjalna strata, nie mówi natomiast jak dotkliwa może być ta strata jeśli już przekroczymy ów próg. Wprowadźmy zatem kolejną miarę, opartą na Value-at-Risk. Warunkową wartość zagrożoną ryzykiem (Expected Shortfall) definiujemy jako średnią wartość strat, które przekraczają Value-at-Risk, dla określonego poziomu istotności oraz horyzontu czasowego. Formalnie możemy to zapisać jako:
$$ \text{ES}_{\alpha} = \mathbb{E} \left[ L \ | \ L \geq \text{VaR}_{\alpha} \right] \text{.} $$
Współczynnik Sharpe’a
Współczynnik Sharpe’a określa stosunek potencjalnego zysku do ryzyka. Im większa wartość tego współczynnika, tym lepsza potencjalna inwestycja. Najczęściej podczas obliczania tego współczynnika jako miarę ryzyka przyjmuje się zmienność mierzoną odchyleniem standardowym stóp zwrotu. Nic jednak nie stoi na przeszkodzie aby wykorzystać inne miary ryzyka do obliczenia współczynnika Sharpe’a. Zdefiniujmy zatem uogólniony współczynnik Sharpe’a w następujący sposób:
$$ \text{Sharpe} \stackrel{\Delta}{=} \frac{\mu \ – \ \mu_F}{\mathcal{R} \left( \mu \right) } \ \text{,} $$
gdzie $\mu$ oznacza stopę zwrotu portfela, $\mu_F$ oznacza stopę procentową wolną od ryzyka (np. oprocentowanie obligacji skarbowych), natomiast $ \mathcal{R} \left( \mu \right) $ oznacza dowolną miarę ryzyka będącą funkcją stóp zwrotu portfela. W tym artykule jako miarę ryzyka przyjmiemy właśnie Value-at-Risk oraz Expected Shortfall, zatem współczynnik Sharpe’a będziemy interpretować jako miarę stosunku potencjalnego zysku do wartości zagrożonej ryzykiem.
Dla uproszczenia stopę procentową wolną od ryzyka przyjmiemy na poziomie 5%.
|
1 |
risk_free = 0.05 |
Analiza danych
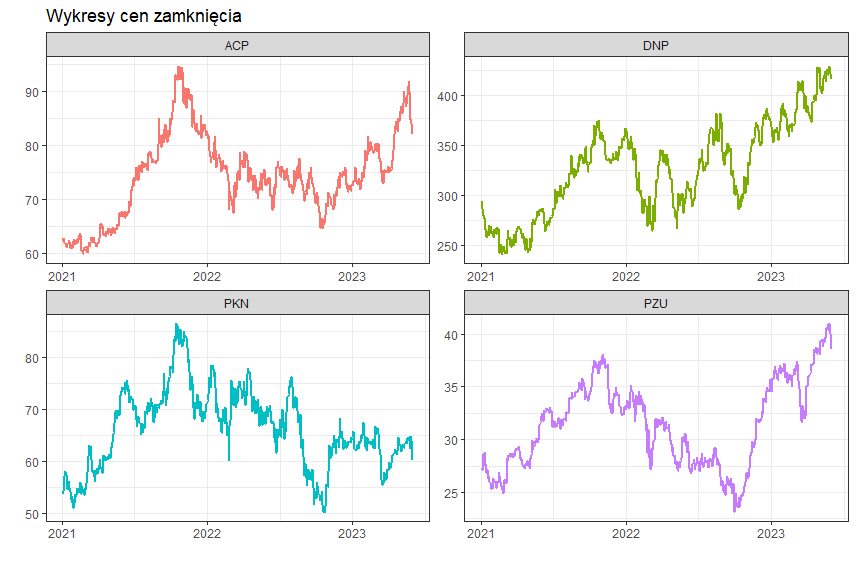
Nasz portfel inwestycyjny będzie składał się z 4 spółek notowanych na Giełdzie Papierów Wartościowych oraz wchodzących w skład indeksu WIG20 (stan na 09.06.2023). Są to następujące spółki: Asseco Poland, Dino Polska, PKN Orlen oraz PZU. Ceny zamknięcia zostały pobrane z portalu stooq.pl. Poniżej widzimy wykresy cen zamknięcia badanych spółek w okresie od stycznia 2021 do maja 2023. Wykresy zostały wykonane przy użyciu biblioteki ggplot2.
Liczymy logarytmiczne stopy zwrotów $r_t = \ln(p_t) \ – \ \ln(p_{t-1})$.
|
1 2 3 4 |
returns_df = sapply( df %>% select(-Data) , function(x) diff(log(x), lag = 1) ) %>% as.data.frame() |
Na podstawie danych historycznych obliczamy zannualizowane stopy zwrotu dla poszczególnych spółek za pomocą wzoru:
$$ \mu_A = \left( \frac{1}{N} \sum_{i=1}^N \mu_i + 1 \right)^{252} \ – \ 1 $$
gdzie $\mu_i$ oznacza dzienne stopy zwrotu, natomiast $N$ oznacza dostępnych dni. Przyjmujemy 252 jako ilość dni roboczych w ciągu roku.
|
1 |
returns_mean = (colMeans(returns_df) + 1)^252 - 1 |
Liczymy Value-at-Risk oraz Expected Shortfall dla poszczególnych spółek w naszym portfelu inwestycyjnym. Przyjmujemy poziom istotności $\alpha = 5\%$.
|
1 2 3 4 5 6 7 8 9 |
alpha = 0.05 returns_var = sapply(returns_df, quantile, probs = alpha) returns_cvar = sapply(1:ncol(returns_df), function(i) { asset_returns = returns_df[, i] asset_var = returns_var[i] cvar_indicator = asset_returns < asset_var cvar = -sum(asset_returns * cvar_indicator) / sum(cvar_indicator) return(cvar) }) |
Interpretacja Value-at-Risk
Poniżej widzimy, że największy zysk w badanym okresie przyniosły spółki Dino Polska oraz PZU, natomiast spółka PKN Orlen przyniosła najmniejszy zysk. Jak interpretujemy Value-at-Risk oraz Expected Shortfall? Omówmy to na przykładzie spółki Dino Polska. W przypadku tej spółki Value-at-Risk wynosi -3.48%. Oznacza to, że w 5% najgorszych scenariuszy (5%, bo tyle wynosi przyjęty przez nas poziom istotności $\alpha$) dzienne obsunięcie kapitału podczas inwestycji w tę spółkę może przekroczyć 3.48%. Natomiast Expected Shortfall dla spółki Dino Polska wynosi -4.64%. Oznacza to, że jeśli zrealizuje się najgorsze 5% scenariuszy, to średnie dzienne obsunięcie kapitału może wynieść aż 4.64%.
| Spółka | Stopa zwrotu $\mu$ | Value-at-Risk | Expected Shortfall |
| Asseco Poland | 12.44% | -2.63% | -3.82% |
| Dino Polska | 15.66% | -3.48% | -4.64% |
| PKN Orlen | 4.99% | -3.70% | -4.96% |
| PZU | 15.63% | -2.94% | -3.93% |
Symulacje Monte Carlo
Przygotowanie środowiska do symulacji
Wylosujemy $N = 10000$ portfeli składających się z tych czterech spółek.
|
1 |
num_of_portfolios = 1e4 |
Inicjalizujemy macierz wymiaru $N \times k$ do przechowywania wag portfela, gdzie $k$ to ilość aktywów.
|
1 |
weights = matrix(nrow = num_of_portfolios, ncol = ncol(returns_df)) |
Inicjalizujemy ramkę danych do przechowywania wyników portfeli: stóp zwrotu portfeli, Value-at-Risk oraz Expected Shortfall dla poszczególnych portfeli oraz współczynnika Sharpe’a określonego dla tych dwóch miar ryzyka.
|
1 2 3 4 5 6 7 |
portfolio_metrics = data.frame( returns = rep(0, num_of_portfolios) , var = rep(0, num_of_portfolios) , sharpe_var = rep(0, num_of_portfolios) , cvar = rep(0, num_of_portfolios) , sharpe_cvar = rep(0, num_of_portfolios) ) |
Ustalamy ziarno generatora liczb losowych dla zapewnienia powtarzalności wyników.
|
1 |
set.seed(2137) |
Przeprowadzenie symulacji
Wykonujemy symulacje według następującej procedury:
- Losujemy $k$ liczb z rozkładu jednostajnego na odcinku $[0, 1]$. Będą to wagi portfela $\omega = [\omega_1, \dots, \omega_k]$.
- Normalizujemy wagi, tak aby ich suma wynosiła $1$, czyli $\omega_i := \frac{\omega_i}{\sum \omega}$.
- Liczymy stopę zwrotu portfela $\mu = \omega^T \mu$, gdzie $\mu = [\mu_1, \dots, \mu_k]$ to zannualizowane stopy zwrotów poszczególnych aktywów.
- Liczymy dzienne stopy zwrotu portfela $\mu_{p_i} = M \omega $, gdzie $M$ jest macierzą wymiaru $n \times k$ przechowującą dzienne stopy zwrotów poszczególnych spółek ($n$ oznacza ilość historycznych dziennych stóp zwrotu branych do analizy).
- Liczymy Value-at-Risk za pomocą metody historycznej, czyli po prostu obliczamy $\alpha$-kwantyl dziennych stóp zwrotu portfela.
- Liczymy współczynnik Sharpe’a dla Value-at-Risk.
- Liczymy ilość przekroczeń, tzn. kiedy dzienna stopa zwrotu portfela była poniżej Value-at-Risk.
- Liczymy Expected Shortfall, czyli średnią stratę w dniach kiedy stopa zwrotu portfela przekroczyła Value-at-Risk.
- Liczymy współczynnik Sharpe’a dla Expected Shortfall.
- Powtarzamy kroki 1-9 $N$ razy.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
for (i in 1:num_of_portfolios) { random_weights = runif(ncol(weights)) random_weights = random_weights / sum(random_weights) weights[i, ] = random_weights portfolio_metrics$returns[i] = random_weights %*% returns_mean portfolio_returns = as.numeric(as.matrix(returns_df) %*% random_weights) portfolio_metrics$var[i] = -quantile(portfolio_returns, alpha) portfolio_metrics$sharpe_var[i] = (portfolio_metrics$returns[i] - risk_free) / portfolio_metrics$var[i] cvar_indicator = portfolio_returns < -portfolio_metrics$var[i] portfolio_metrics$cvar[i] = -sum(portfolio_returns * cvar_indicator) / sum(cvar_indicator) portfolio_metrics$sharpe_cvar[i] = (portfolio_metrics$returns[i] - risk_free) / portfolio_metrics$cvar[i] } |
Ekstrakcja wyników
Wyniki powyższej symulacji zostały zapisane we wcześniej utworzonej ramce danych oraz w macierzy wag. Musimy zatem wyciągnąć cztery portfele spełniające nasze kryteria optymalizacyjne, tzn. portfel o najmniejszej wartości Value-at-Risk, najmniejszej wartości Expected Shortfall oraz portfele najwyższym współczynniku Sharpe’a dla obu miar ryzyka.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
optimal_portfolios = data.frame( Min_VaR = c( round(100*weights[which.min(portfolio_metrics$var),], 2) ,round(100*portfolio_metrics[which.min(portfolio_metrics$var), ], 2) %>% as.numeric() ) ,Max_Sharpe_VaR = c( round(100*weights[which.max(portfolio_metrics$sharpe_var),], 2) ,round(100*portfolio_metrics[which.max(portfolio_metrics$sharpe_var), ], 2) %>% as.numeric() ) ,Min_cVaR = c( round(100*weights[which.min(portfolio_metrics$cvar),], 2) ,round(100*portfolio_metrics[which.min(portfolio_metrics$cvar), ], 2) %>% as.numeric() ) ,Max_Sharpe_cVaR = c( round(100*weights[which.max(portfolio_metrics$sharpe_cvar),], 2) ,round(100*portfolio_metrics[which.max(portfolio_metrics$sharpe_cvar), ], 2) %>% as.numeric() ) ) %>% t() %>% as.data.frame() |
Portfele optymalne
Portfel o najmniejszej wartości Value-at-Risk jest stosunkowo zrównoważony. Spółki Asseco Poland oraz Dino Polska mają w nim największy udział, wynoszący odpowiednio 36% oraz 32%. Stosunkowo wysoki jest również udział PZU, wynoszący 18%. W przypadku tego portfela roczna stopa zwrotu wynosi 13.11%, natomiast w 5% najgorszych scenariuszy dzienne obsunięcie kapitału może przekroczyć 1.84%. Jeśli już zostanie ten poziom przekroczony, to średnia strata moze wynieść aż 2.66%.
Portfel o najlepszym stosunku zysku do ryzyka, gdzie miarą ryzyka jest Value-at-Risk, zawierał znacznie wyższy udział spółki PZU (36%) oraz znacząco niższy udział spółki PKN Orlen (1%). Cechował się również nieco wyższą wartość Value-at-Risk (1.90%) w porównaniu do portfela o najmniejszej wartości Value-at-Risk, ale także wyższą stopą zwrotu (14.45%), co jest zgodne z zasadą, że większe ryzyko może wiązać się z wyższymi potencjalnymi zyskami.
Portfel o najmniejszej wartości Expected Shortfall swoim składem jest podobny do portfela o najmniejszej wartości Value-at-Risk. Możemy zauwazyć z nieco większy udział spółki PZU oraz mniejszy udział spółki Dino Polska. W przypadku tego portfela roczna stopa zwrotu wynosi 13.36%, natomiast w 5% najgorszych scenariuszy dzienne obsunięcie kapitału może przekroczyć 1.88%. Jeśli już zostanie ten poziom przekroczony, to średnia strata moze wynieść aż 2.65%.
Portfel o najlepszym stosunku zysku do ryzyka, gdzie miarą ryzyka jest Expected Shortfall, zawierał prawie zerowy udział spółki PKN Orlen. Mimo to można uznać ten portfel za dobrze zdywersyfikowany, ponieważ zawiera mniej więcej równe udziały trzech pozostałych spółek giełdowych. Portfel ten cechował się również nieco wyższą wartością Exptected Shortfall (2.70%) w porównaniu do portfela o najmniejszej wartości Exptected Shortfall, ale także wyższą stopą zwrotu (14.55%), co również w tym przypadku jest zgodne z zasadą, że większe ryzyko może wiązać się z wyższymi potencjalnymi zyskami.
| Portfel o najmniejszym VaR | Portfel o największym Sharpe VaR | Portfel o najmniejszym ES | Portfel o największym Sharpe ES | |
| Stopa zwrotu | 13.11% | 14.45% | 13.36% | 14.55% |
| Value-at-Risk | 1.84% | 1.90% | 1.88% | 1.97% |
| Współczynnik Sharpe’a (VaR) | 4.40 | 4.96 | 4.44 | 4.84 |
| Expected Shortfall | 2.66% | 2.70% | 2.65% | 2.70% |
| Współczynnik Sharpe’a (ES) | 3.05 | 3.50 | 3.16 | 3.54 |
| Udział % Asseco Poland | 36.4% | 33.28% | 36.62% | 33.78% |
| Udział % Dino Polska | 32.83% | 29.7% | 29.36% | 33.56% |
| Udział % PKN Orlen | 12.81% | 1.16% | 10.4% | 0.06% |
| Udział % PZU | 17.96% | 35.85% | 23.62% | 32.6% |
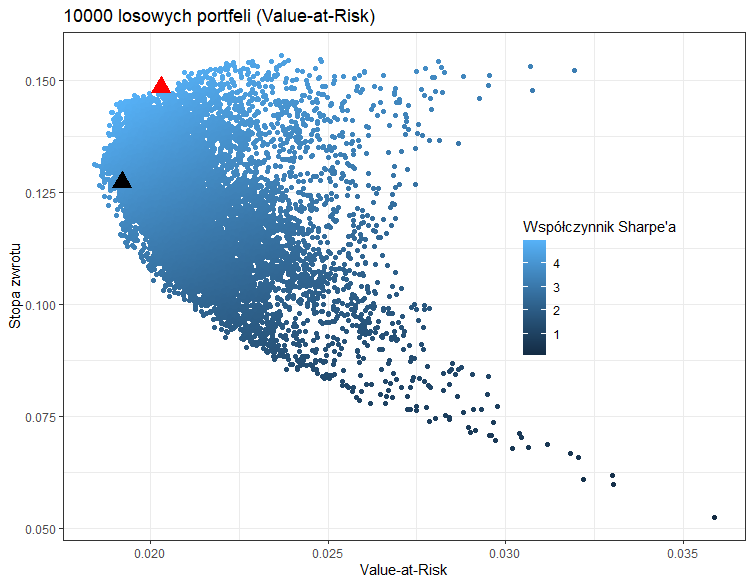
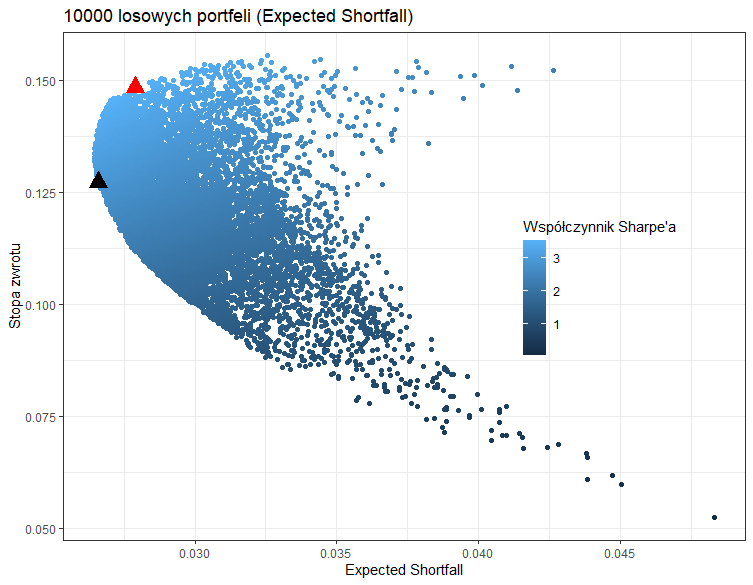
Poniżej widzimy wizualizację wylosowanych portfeli wykonaną za pomocą biblioteki ggplot2. Na osi odciętych mamy miary ryzyka (odpowiednio Value-at-Risk oraz Exptected Shortfall), natomiast na osi rzędnych mamy stopy zwrotów wylosowanych portfeli. Jaśniejszy kolor punktu oznacza korzystniejszy stosunek zysku do ryzyka. Czerwonym trójkątem zaznaczono portfel o najwyższym współczynniku Sharpe’a, natomiast czarnym trójkątem zaznaczono portfel o najmniejszym ryzyku, gdzie miarami ryzyka sa odpowiednio Value-at-Risk oraz Exptected Shortfall.
Warto zauważyć, że zbiór portfeli optymalnych (czyli lewa krawędź zbioru wszystkich portfeli) w przypadku Value-at-Risk jest lekko „poszarpany”, natomiast w przypadku Expected Shortfall oraz w przypadku zmienności mierzonej odchyleniem standardowym stóp zwrotu zbiór portfeli optymalnych tworzy „gładką linię”. Wynika to z matematycznego faktu mówiącego, że w przypadku Value-at-Risk zbiór portfeli optymalnych nie tworzy zbioru wypukłego. Wówczas niemożliwe jest znalezienie optimum globalnego metodami analitycznymi. Zatem jednym z rozwiązań takich zadań optymalizacyjnych jest właśnie zastosowanie metod Monte Carlo.

Pełny kod R można znaleźć na Github.
