Value-at-Risk dla różnych horyzontów czasowych

Wartość zagrożoną ryzykiem, czyli Value-at-Risk możemy obliczyć na wiele różnych sposobów. W kontekście analiz giełdowych zazwyczaj korzystamy z dziennych stóp zwrotu i obliczamy VaR na kolejny dzień. Możemy jednak policzyć VaR dla dalszych horyzontów czasowych, np. tydzień, miesiąc, rok. I tu również istnieje wiele różnych metod obliczeniowych. W tym artykule omówimy dwie popularne metody: pierwiastek kwadratowy z czasu (ang. square root of time) oraz symulacje Monte Carlo. Obliczymy również Value-at-Risk bazując na tygodniowych stopach zwrotu, aby porównać wyniki.

Analiza danych

Przygotowanie danych

Pobieramy dane dotyczące spółki Dino Polska ze strony stooq.pl w interwale dziennym oraz w interwale tygodniowym. Podczas pisania tego artykułu dane obejmują zakres od 20 kwietnia 2017 do 30 czerwca 2023. Jeśli puścisz poniższy kod ponownie dla spółki Dino Polska (lub dla jakiejkolwiek innej spółki giełdowej) to otrzymane przez Ciebie wyniki obliczeń mogą się różnić, ponieważ uwzględnisz świeższe dane w swoich analizach.

Po pobraniu danych giełdowych liczymy logarytmiczne stopy zwrotu dla obu zbiorów danych.

df_daily = read.csv(url('https://stooq.pl/q/d/l/?s=dnp&i=d'), stringsAsFactors = FALSE) %>%
  mutate(Data = as.Date(Data)) %>%
  mutate(Returns = c(NA, diff(log(Zamkniecie)))) %>%
  mutate(Frequency = 'Daily') %>%
  na.omit()

df_weekly = read.csv(url('https://stooq.pl/q/d/l/?s=dnp&i=w'), stringsAsFactors = FALSE) %>%
  mutate(Data = as.Date(Data)) %>%
  mutate(Returns = c(NA, diff(log(Zamkniecie)))) %>%
  mutate(Frequency = 'Weekly') %>%
  na.omit()

df_daily = read.csv(url('https://stooq.pl/q/d/l/?s=dnp&i=d'), stringsAsFactors = FALSE) %>%

mutate(Data = as.Date(Data)) %>%

mutate(Returns = c(NA, diff(log(Zamkniecie)))) %>%

mutate(Frequency = 'Daily') %>%

na.omit()

df_weekly = read.csv(url('https://stooq.pl/q/d/l/?s=dnp&i=w'), stringsAsFactors = FALSE) %>%

mutate(Data = as.Date(Data)) %>%

mutate(Returns = c(NA, diff(log(Zamkniecie)))) %>%

mutate(Frequency = 'Weekly') %>%

na.omit()

Histogramy stóp zwrotu

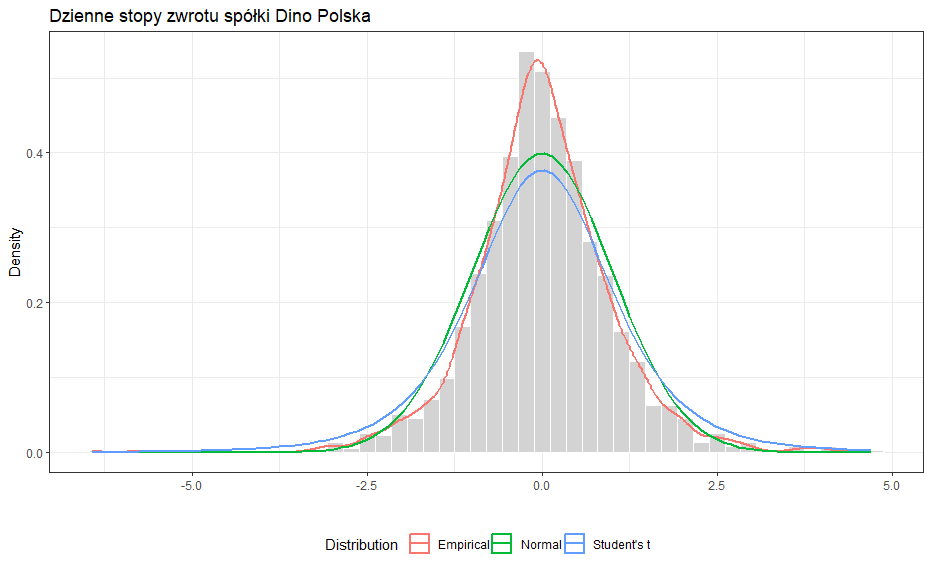
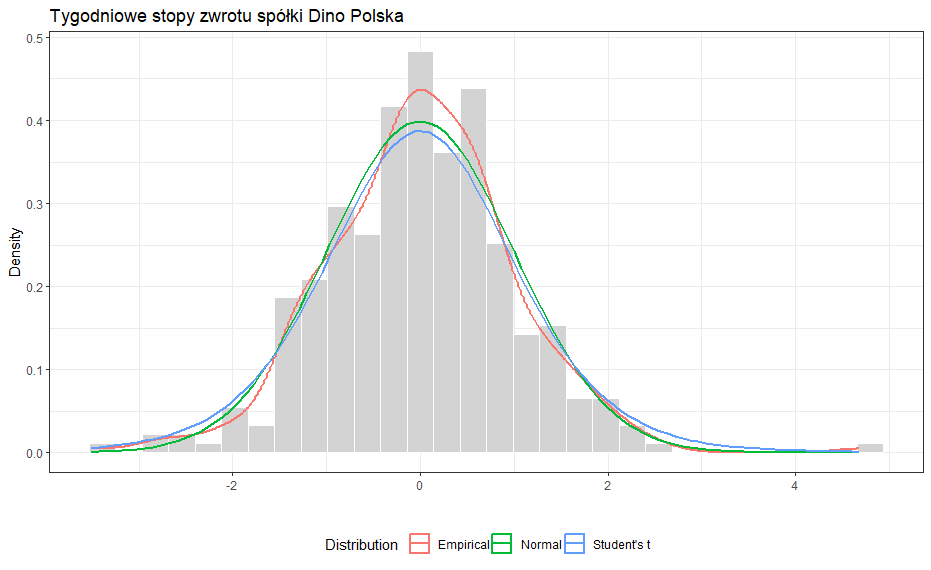
Dla obu szeregów czasowych stóp zwrotu robimy histogram za pomocą biblioteki ggplot2. Do każdego histogramu dodajemy następujące linie:

gęstość empiryczna badanego szeregu czasowego (kolor czerwony)
gęstość teoretyczna dopasowanego rozkładu normalnego (kolor zielony)
gęstość teoretyczna dopasowanego rozkładu t-Studenta (kolor niebieski).

source('https://raw.githubusercontent.com/pawel-wieczynski/useful-functions/main/histogram_with_densities.R')
histogram_with_densities(df_daily, 'Returns', 'Dzienne stopy zwrotu spółki Dino Polska', 50)
histogram_with_densities(df_weekly, 'Returns', 'Tygodniowe stopy zwrotu spółki Dino Polska', 30)

source('https://raw.githubusercontent.com/pawel-wieczynski/useful-functions/main/histogram_with_densities.R')

histogram_with_densities(df_daily, 'Returns', 'Dzienne stopy zwrotu spółki Dino Polska', 50)

histogram_with_densities(df_weekly, 'Returns', 'Tygodniowe stopy zwrotu spółki Dino Polska', 30)

Na wykresach możemy zuważyć, że w przypadku danych o interwale tygodniowym, oba rozkłady teoretyczne wydają się być lepiej dopasowane niż dla danych o interwale dziennym. W dalszej części artykułu będziemy korzystać z rozkładu normalnego, aczkolwiek większość obliczeń można potwórzyć korzystając z innych rozkładów statystycznych.

dino polska histogram d dino polska histogram w

Dopasowanie rozkładu normalnego

Dopasujmy zatem parametry rozkładu normalnego (tj. średnią oraz odchylenie standardowe) dla obu szeregów czasowych. W tym przypadku otrzymaliśmy następujące wartości:

dla danych dziennych średnia stopa zwrotu wynosi 0.164%, natomiast odchylenie standardowe stóp zwrotu wynosi 0.0234
dla danych tygodniowych średnia stopa zwrotu wynosi 0.77%, natomiast odchylenie standardowe stóp zwrotu wynosi 0.0486.

m_daily = mean(df_daily$Returns)
round(m_daily, 4)
# 0.0016

sd_daily = sd(df_daily$Returns)
round(sd_daily, 4)
# 0.0234

m_weekly = mean(df_weekly$Returns)
round(m_weekly, 4)
# 0.0077

sd_weekly = sd(df_weekly$Returns)
round(sd_weekly, 4)
# 0.0486

m_daily = mean(df_daily$Returns)

round(m_daily, 4)

# 0.0016

sd_daily = sd(df_daily$Returns)

round(sd_daily, 4)

# 0.0234

m_weekly = mean(df_weekly$Returns)

round(m_weekly, 4)

# 0.0077

sd_weekly = sd(df_weekly$Returns)

round(sd_weekly, 4)

# 0.0486

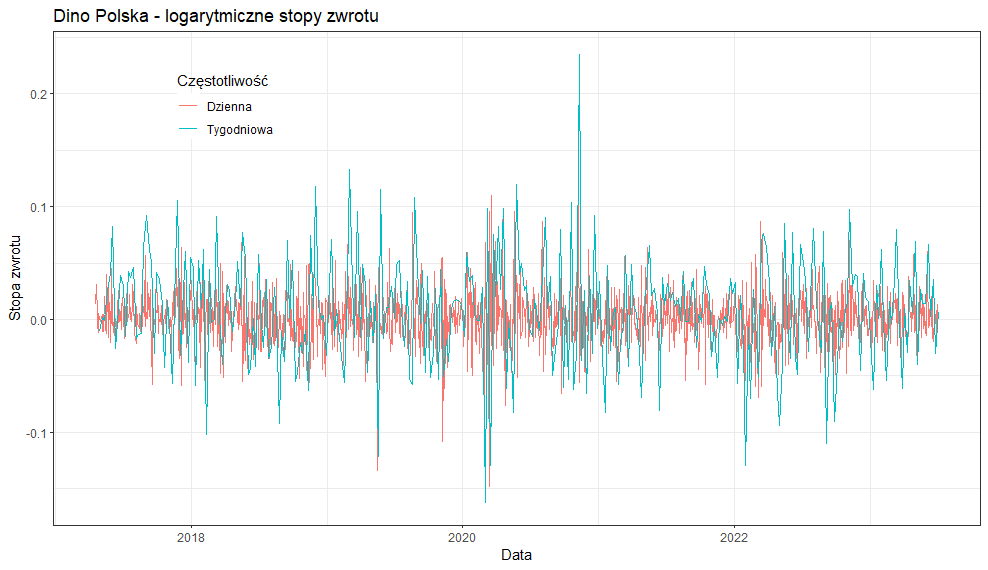
Warto zwrócić szczególną uwagę, że dane w interwale tygodniowym mają wyższą zmienność niż dane w interwale dziennym. Czy jest to przypadek?

Częstotliwość danych a zmienność stóp zwrotu

Poniżej widzimy wykres logarytmicznych stóp zwrotu wykonany za pomocą biblioteki ggplot2. Na wykresie łatwo zauważyć, że dane w interwale tygodniowym mają wyższą zmienność niż dane w interwale dziennym. Jest to dosyć powszechne zjawisko, ponieważ w ciągu tygodnia ceny mają więcej czasu aby wzrosnąć lub spaść niż w ciągu jednego dnia. To samo dotyczy dłuższych interwałów, np. miesiąc, kwartał, rok.

dnp log zwroty

Dla formalności wykonajmy jeszcze test na równość wariancji. W tym teście mamy następujące hipotezy:

Hipoteza zerowa ($H_0$): oba szeregi mają jednakową wariancję
Hipoteza alternatywna ($H_1$): szereg w interwale tygodniowym ma większą wariancję niż szereg w interwale dziennym.

Aby wykonać test wariancji dla dwóch próbek w RStudio, korzystamy z funkcji var.test(). W naszym przypadku otrzymaliśmy wartość p-value mniejsza od 0.05, zatem odrzucamy hipotezę zerową. Możemy zatem formalnie stwierdzić, że dane o mniejszej częstotliwości mają większą zmienność niż dane o większej częstotliwości.

var.test(
  df_weekly$Returns
  , df_daily$Returns
  , ratio = 1
  , alternative = 'greater'
)

var.test(

df_weekly$Returns

, df_daily$Returns

, ratio = 1

, alternative = 'greater'

)

Pamiętajmy jednak, że test na równość wariancji zakłada, że próbki mają rozkład normalny, co w przypadku naszych danych niekoniecznie jest prawdą.

Skumulowane stopy zwrotu

Oznaczmy $r_t$ jako logarytmiczną stopę zwrotu w chwili $t$, tzn. $r_t = \ln (P_t) \ – \ \ln (P_{t-1}) $, gdzie $P_t$ oznacza cenę zamknięcia danej spółki giełdowej w chwili $t$. W kontekście naszych analiz $t-1$ będzie oznaczał poprzednią sesję giełdową (dla danych w interwale dziennym) lub sesję giełdową z tygodnia wstecz (dla danych w interwale tygodniowym). Oznaczmy $h=1, \dots , H$ jako horyzont czasowy dla którego będziemy prognozować Value-at-Risk. Jeśli $r_h$ zą niezależne oraz mają ten sam rozkład statystyczny, to skumulowana stopa zwrotu wynosi:

$$ y_H = \sum_{h=1}^H r_h $$

Zastosowanie zwykłej sumy wynika z faktu, że korzystamy z logarytmicznych stóp zwrotu. Gdybyśmy korzystali ze prostych stóp zwrotu, wówczas (przy pewnych modyfikacjach wzoru) musielibyśmy skorzystać z iloczynu zamiast z sumy. A to z kolei spowodowałoby mniej dokładne wyniki, ponieważ mnożenie dużej liczby ułamków mniejszych od 1 (a stopy zwrotu są zazwyczaj wyrażane w takich właśnie ułamkach) prowadzi do zaokrągleń, które kumulują się wraz z ilością wykonanych operacji mnożenia. Addytywność jest jednym z powodów dla których w analizach finansowych korzystamy z logarytmicznych stóp zwrotu. Należy jednak pamiętać, że ostatecznie inwestorzy są zainteresowani prostymi stopami zwrotów a nie ich logarytmicznymi odpowiednikami.

Jeśli stopy zwrotu $r_h$ są niezależne oraz mają rozkład normalny o jednakowej średniej $\mu$ i jednakowym odchyleniu standardowym $\sigma$, wówczas rozkład skumulowanej stopy zwrotu ma rozkład normalny o następujących parametrach:

średnia stopa zwrotu wynosi $\mu_H = H\mu$
odchylenie standardowe stóp zwrotu wynosi $ \sigma_H = \sqrt{H} \sigma $

Value-at-Risk dla $h > 1$

Pierwiastek kwadratowy z czasu

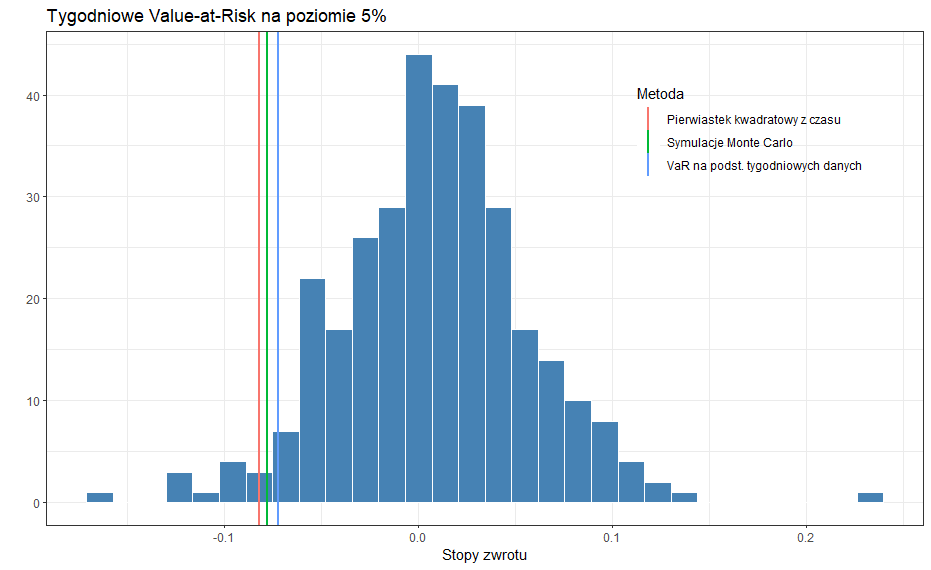
Pierwszą metodą, którą omówimy jest tzw. pierwiastek kwadratowy z czasu. Metoda ta wynika wprost z wcześniejszego stwierdzenia, że dla skumulowanej stopy zwrotu odchylenie standardowe wynosi $\sqrt{H} \sigma$. Przypomnijmy, że jeśli stopy zwrotu $r_h$ mają rozkład normalny, to Value-at-Risk definiujemy jako $\alpha$-kwantyl tego rozkładu. Przyjmijmy poziom istotności wynoszący $\alpha = 5\%$. Zatem dla naszych danych Value-at-Risk dla $h=1$ wynosi 3.68% w przypadku danych dziennych oraz 7.22% dla danych tygodniowych.

VaR_daily = qnorm(alpha, m_daily, sd_daily)
round(100*VaR_daily, 2)
# -3.68

VaR_weekly = qnorm(alpha, m_weekly, sd_weekly)
round(100*VaR_weekly, 2)
# -7.22

VaR_daily = qnorm(alpha, m_daily, sd_daily)

round(100*VaR_daily, 2)

# -3.68

VaR_weekly = qnorm(alpha, m_weekly, sd_weekly)

round(100*VaR_weekly, 2)

# -7.22

Oby obliczyć tygodniowe Value-at-Risk na podstawie dziennych stóp zwrotu, przyjmujemy $H=5$ (ponieważ tydzień ma zazwyczaj 5 sesji giełdowych), a następnie obliczamy $\textit{VaR}_{\textit{daily}} \ \sqrt{H}$. W tym przypadku otrzymujemy Value-at-Risk wynoszące 8.22%.

H = 5
VaR_daily_H = VaR_daily * sqrt(H)
round(100*VaR_daily_H, 2)
# -8.22

H = 5

VaR_daily_H = VaR_daily * sqrt(H)

round(100*VaR_daily_H, 2)

# -8.22

Symulacje Monte Carlo

Drugą omawianą metodą są symulacje Monte Carlo. Na temat podstaw metod Monte Carlo możesz przeczytać na naszym blogu. W tym przypadku zakładamy, że badane stopy zwrotu mają pewien rozkład lub że istnieje jakiś proces za pomocą którego możemy generować te stopy zwrotu (np. szereg klasy ARIMA-GARCH). W tym artykule ograniczamy się do założenia, że stopy zwrotu mają rozkład normalny.

Aby obliczyć Value-at-Risk za pomocą symulacji Monte Carlo postępujemy według następującej procedury:

Generujemy ścieżkę stóp zwrotu $r_1, \dots, r_H$ dla wybranego horyzontu czasowego $H$
Liczymy skumulowaną stopę zwrotu $y_H = \sum_{h=1}^H r_h$ (pamiętajmy, że dodawania działa tylko w przypadku logarytmicznych stóp zwrotu)
Powtarzamy kroki 1-2 $N$ razy.
Obliczamy $\alpha$-kwantyl z $N$ wartości $y_H$.

Przyjmijmy $N=10000$. Inicjalizujemy wektor do przechowywania wyników, tzn. symulowanych wartości $y_H$. Następnie ustalamy ziarno generatora liczb losowych dla zapewnienia powtarzalności wyników i wykonujemy symulacje Monte Carlo według procedury opisanej powyżej.

N = 1e4
simulated_weekly_returns = c()

set.seed(2137)
for (i in 1:N) {
  returns = rnorm(H, m_daily, sd_daily)
  cum_return = sum(returns)
  simulated_weekly_returns = c(simulated_weekly_returns, cum_return)
}

N = 1e4

simulated_weekly_returns = c()

set.seed(2137)

for (i in 1:N) {

returns = rnorm(H, m_daily, sd_daily)

cum_return = sum(returns)

simulated_weekly_returns = c(simulated_weekly_returns, cum_return)

}

W tym przypadku Value-at-Risk na najbliższy tydzień wynosi 7.78%.

VaR_MC = quantile(simulated_weekly_returns, alpha)
round(100*VaR_MC, 2)
# -7.78

VaR_MC = quantile(simulated_weekly_returns, alpha)

round(100*VaR_MC, 2)

# -7.78

Porównanie wyników

Obliczyliśmy Value-at-Risk na najbliższy tydzień za pomocą trzech metod.

Na podstawie historycznych stóp zwrotu o interwale tygodniowym, założyliśmy, że mają one rozkład normalny i obliczyliśmy Value-at-Risk dla $h=1$ czyli na kolejny tydzień. Otrzymaliśmy wynik 7.22% na poziomie istotności $\alpha$ wynoszącym 5%. Oznacza to, że inwestując w spółkę Dino Polska z 95% prawdopodobieństwem obsunięcie kapitału w najbliższym tygodniu nie przekroczy 7.22% wartości inwestycji.

Korzystając z historycznych stóp zwrotu o interwale dziennym obliczyliśmy Value-at-Risk na najbliższy tydzień, tzn. na najbliższe 5 sesji giełdowych. Wynik otrzymany metodą analityczną (pierwiastek kwadratowy z czasu) wynosi 8.22%, natomiast wynik otrzymany metodą numeryczną (symulacje Monte Carlo) wynosi 7.78%. Interpretacje tych wyników są takie same jak powyżej.

Widzimy zatem, że wyniki otrzymane różnymi metodami dają podobne rezultaty. Dlaczego zatem korzystamy z dziennych stóp zwrotu i obliczamy VaR dla dalszych horyzontów czasowych, zamiast po prostu skorzystać z tygodniowych stóp zwrotu? Otóż dzienne stopy zwrotu zapewniają nam większą elastyczność. Korzystając z nich możemy policzyć Value-at-Risk w dowolnym horyzoncie czasowym, np. 8 dni, co byłoby trudne do uzyskania bazując na tygodniowych stopach zwrotu.

value at risk time horizon

Value-at-Risk dla $h = 1, \dots , 252$

Sprawdźmy zatem jak powyższe metody sprawdzają się dla $h$ wynoszącego od 1 do 252. W tym kontekście 252 oznacza pełny rok kalendarzowy, ponieważ tyle średnio jest sesji giełdowych w danym roku.

H = 1:252
VaR_year = VaR_daily * sqrt(H)

VaR_year_MC = c()

set.seed(2137)
for (h in H) {
  simulated_returns = c()
  for (i in 1:N) {
    returns = rnorm(h, m_daily, sd_daily)
    cum_return = sum(returns)
    simulated_returns = c(simulated_returns, cum_return)
  }
  VaR_year_MC[h] = quantile(simulated_returns, alpha)
}

H = 1:252

VaR_year = VaR_daily * sqrt(H)

VaR_year_MC = c()

set.seed(2137)

for (h in H) {

simulated_returns = c()

for (i in 1:N) {

returns = rnorm(h, m_daily, sd_daily)

cum_return = sum(returns)

simulated_returns = c(simulated_returns, cum_return)

}

VaR_year_MC[h] = quantile(simulated_returns, alpha)

}

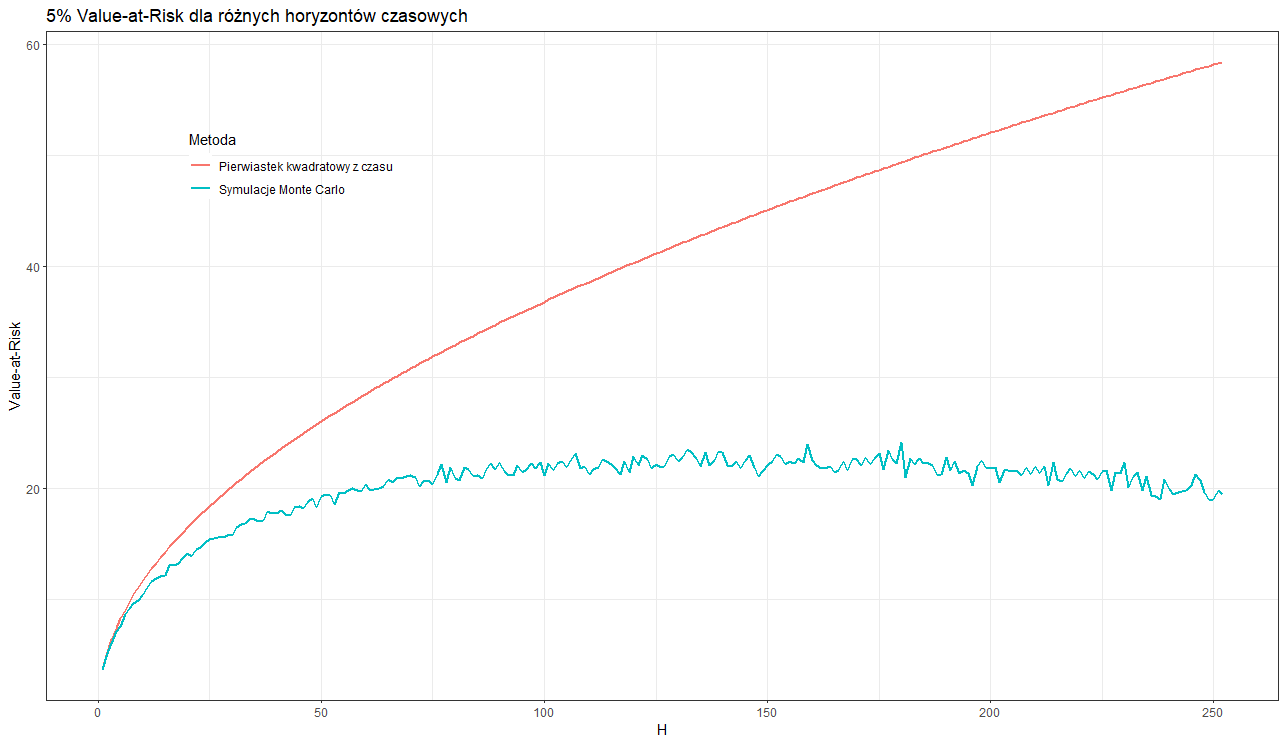
Na poniższym wykresie widzimy Value-at-Risk dla różnych horyzontów czasowych obliczone dwoma metodami opisanymi w tym artykule. W przypadku pierwszej metody (pierwiastek kwadratowy z czasu) ryzyko rośnie wraz z czasem, co jest zgodne z intuicją oraz z praktyką rynkową.

W przypadku symulacji Monte Carlo ryzyko stabilizuje się na poziomie około 20%. Oznacza to, że nieważne na jak długo zainwestujemy pieniądze w spółkę Dino Polska, mamy 95% prawdopodobieństwo, że obsunięcie kapitału nie przekroczy 20%.

Możemy zauważyć, że dla krótkich horyzontów czasowych wyniki obu metod są na podobnym poziomie. W przypadku tych danych zgodność występuje dla $h$ od 1 do 7. Która metoda zatem jest lepsza dla dłuższych horyzontów czasowych? Zastanówmy się co nam podpowiada intuicja oraz doświadczenie rynkowe. Pierwsza metoda jest zgodna z intuicją, że im dłuższa inwestycja tym większe ryzyko. Natomiast funkcja pierwiastka dąży do nieskończoności, w szczególności w pewnym momencie funkcja ta przekracza wartość 100%. Jednak zajmując długie pozycje na akcjach giełdowych, nasza strata nie może przekroczyć 100%. Z kolei w przypadku symulacji Monte Carlo ryzyko się stabilizuje na pewnym poziomie co jest sprzeczne z intuicją. Ponadto, w przypadku bankructwa spółki (co jest niezwykle mało prawdopodobne), strata może wynieść aż do 100%.

Pamiętajmy jednak, korzystaliśmy z założenia, że stopy zwrotu mają rozkład normalny. W praktyce takie założenie jest spełnione niezwykle rzadko. Bardziej interesujące, bardziej przydatne w praktyce oraz nierzadko bardziej wiarygodne wyniki możemy uzyskać korzystając z bardziej zaawansowanych metod obliczania Value-at-Risk. Na temat niektórych metod obliczania Value-at-Risk możesz przeczytać na naszym blogu.

value at risk h1 252