Optymalizacja portfela metodami Monte Carlo
W tym wpisie przedstawimy optymalizację portfela metodami Monte Carlo w przy użyciu języka R oraz programu RStudio. Przyjmiemy dwa kryteria optymalizacyjne: minimalizję zmienności mierzonej odchyleniem standardowym oraz maksymalizację współczynnika Sharpe’a określającego stosunek zysku do ryzyka. Przykładowy portfel będzie się składał z akcji czterech spółek notowanych na GPW oraz wchodzących w skład indeksu WIG20 (stan na 09.06.2023): Asseco Poland, Dino Polska, PKN Orlen oraz PZU.
Analiza danych
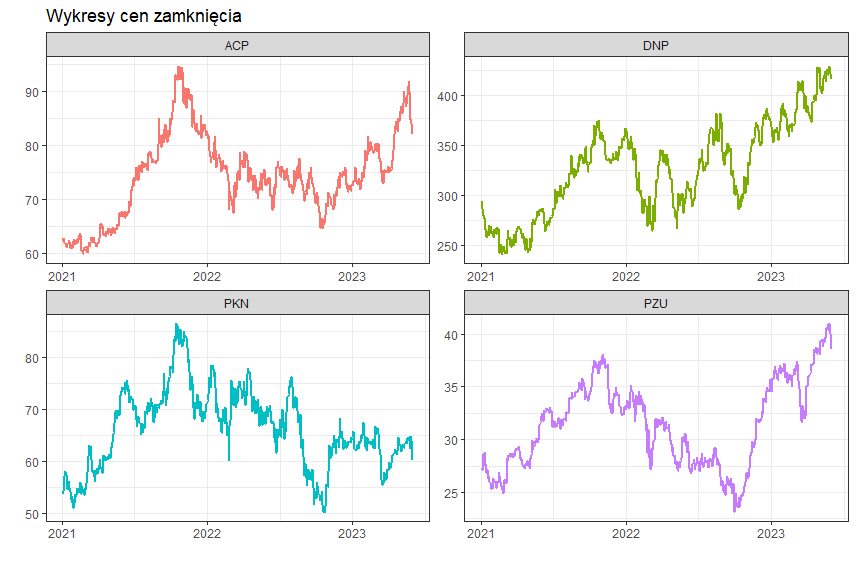
Poniżej widzimy wykresy cen zamknięcia badanych spółek w okresie od stycznia 2021 do maja 2023. Wykresy zostały wykonane przy użyciu biblioteki ggplot2.
Liczymy logarytmiczne stopy zwrotów $r_t = \ln(p_t) \ – \ \ln(p_{t-1})$.
|
1 2 3 4 |
returns_df = sapply( df %>% select(-Data) , function(x) diff(log(x), lag = 1) ) %>% as.data.frame() |
Na podstawie danych historycznych obliczamy zannualizowaną stopę zwrotu, zannualizowaną macierz kowariancji oraz zmienność stóp zwrotu.
|
1 2 3 |
returns_mean = (colMeans(returns_df) + 1)^252 - 1 returns_cov = cov(returns_df) * 252 returns_sd = diag(returns_cov) %>% sqrt() |
Poniżej widzimy, że największy zysk w badanym okresie przyniosły spółki Dino Polska oraz PZU. Natomiast spółka PKN Orlen przyniosła najmniejszy zysk, a jej stopy zwrotu cechowały się największą zmiennością.
| Spółka | Stopa zwrotu $\mu$ | Zmienność $\sigma$ |
| Asseco Poland | 12.44% | 27.56 |
| Dino Polska | 15.66% | 33.50 |
| PKN Orlen | 4.99% | 36.00 |
| PZU | 15.63% | 28.98 |
Symulacje Monte Carlo
Przygotowanie środowiska do symulacji
Współczynnik Sharpe’a określający stosunek zysku do ryzyka dany jest wzorem
$$\text{Sharpe} = \frac{\mu_R \ – \ \mu_F}{\sigma_R} \ \text{,}$$
gdzie $\mu_R$ oraz $\sigma_R$ oznaczają odpowiednio stopę zwrotu portfela oraz zmienność portfela, natomiast $\mu_F$ oznacza stopę wolną od ryzyka. Dla uproszczenia przyjmijmy zatem stopę wolną od ryzyka $\mu_F$ wynoszącą $5\%$ w skali roku. W praktyce jako benchmark stopy wolnej od ryzyka przyjmuje się stopę oprocentowania obligacji skarbowych albo WIBOR.
|
1 |
risk_free = 0.05 |
Wylosujemy $n = 10000$ portfeli składających się z tych czterech spółek.
|
1 |
num_of_portfolios = 1e4 |
Inicjalizujemy macierz wymiaru $n \times k$ do przechowywania wag portfela, gdzie $k$ to ilość aktywów.
|
1 |
weights = matrix(nrow = num_of_portfolios, ncol = ncol(returns_df)) |
Inicjalizujemy ramkę danych do przechowywania wyników portfeli: stóp zwrotu, zmienności oraz współczynnika Sharpe’a.
|
1 2 3 4 5 |
portfolio_metrics = data.frame( returns = rep(0, num_of_portfolios) , volatility = rep(0, num_of_portfolios) , sharpe = rep(0, num_of_portfolios) ) |
Ustalamy ziarno generatora liczb losowych dla zapewnienia powtarzalności wyników.
|
1 |
set.seed(2137) |
Przeprowadzenie symulacji
Wykonujemy symulacje według następującej procedury:
- Losujemy $k$ liczb z rozkładu jednostajnego na odcinku $[0, 1]$. Będą to wagi portfela $\omega = [\omega_1, \dots, \omega_k]$.
- Normalizujemy wagi, tak aby ich suma wynosiła $1$, czyli $\omega_i := \frac{\omega_i}{\sum \omega}$.
- Liczymy stopę zwrotu portfela $\mu_R = \omega^T \mu$, gdzie $\mu = [\mu_1, \dots, \mu_k]$ to zannualizowane stopy zwrotów poszczególnych aktywów.
- Liczymy zmienność stóp zwrotu portfela $\sigma_R = \sqrt{\omega^T C \omega}$, gdzie $C$ to zannualizowana macierz kowariancji stóp zwrotu.
- Liczymy współczynnik Sharpe’a.
- Powtarzamy kroki 1-5 $n$ razy.
|
1 2 3 4 5 6 7 8 9 10 11 |
for (i in 1:num_of_portfolios) { random_weights = runif(ncol(weights)) random_weights = random_weights / sum(random_weights) weights[i, ] = random_weights portfolio_metrics$returns[i] = random_weights %*% returns_mean portfolio_metrics$volatility[i] = sqrt(t(random_weights) %*% (returns_cov %*% random_weights)) portfolio_metrics$sharpe[i] = (portfolio_metrics$returns[i] - risk_free) / portfolio_metrics$volatility[i] } |
Ekstrakcja wyników
Wyniki powyższej symulacji zostały zapisane we wcześniej utworzonej ramce danych oraz w macierzy wag. Musimy zatem wyciągnąć dwa portfele spełniające nasze kryteria optymalizacyjne, tzn. portfel o najmniejszej zmienności mierzonej odchyleniem standardowym oraz portfel o najwyższym współczynniku Sharpe’a.
|
1 2 3 4 5 6 7 8 9 10 |
optimal_portfolios = data.frame( Min_Variance = c( round(100 * weights[which.min(portfolio_metrics$volatility),], 2) ,round(100 * portfolio_metrics[which.min(portfolio_metrics$volatility), ], 2) %>% as.numeric() ) ,Max_Sharpe = c( round(100 * weights[which.max(portfolio_metrics$sharpe),], 2) ,round(100 * portfolio_metrics[which.max(portfolio_metrics$sharpe), ], 2) %>% as.numeric() ) ) %>% t() %>% as.data.frame() |
Portfele optymalne
Portfel o najmniejszej zmienności był zdywersyfikowany, posiadając od 15% do 40% udziału poszczególnych spółek. Portfel o najwyższym współczynniku Sharpe’a praktycznie w ogóle nie zawierał spółki PKN Orlen oraz miał mniejszy udział spółki Asseco Poland na korzyść udziału spółek Dino Polska oraz PZU. Portfel ten cechował się wyższą stopą zwrotu, ale również wyższą zmiennością stóp zwrotu niż portfel o najmniejszej zmienności. Potwierdza to zasadę, że im większe ryzyko (w tym przypadku zmienność), tym większy potencjalny zysk.
| Portfel o najmniejszej zmienności | Portfel o najwyższym współczynniku Sharpe’a | |
| Stopa zwrotu | 12.73% | 14.84% |
| Zmienność | 20.17 | 21.39 |
| Współczynnik Sharpe’a | 38.33 | 46.03 |
| Udział % Asseco Poland | 39.87% | 24.69% |
| Udział % Dino Polska | 24.20% | 36.14% |
| Udział % PKN Orlen | 15.34% | 0.07% |
| Udział % PZU | 20.59% | 39.11% |
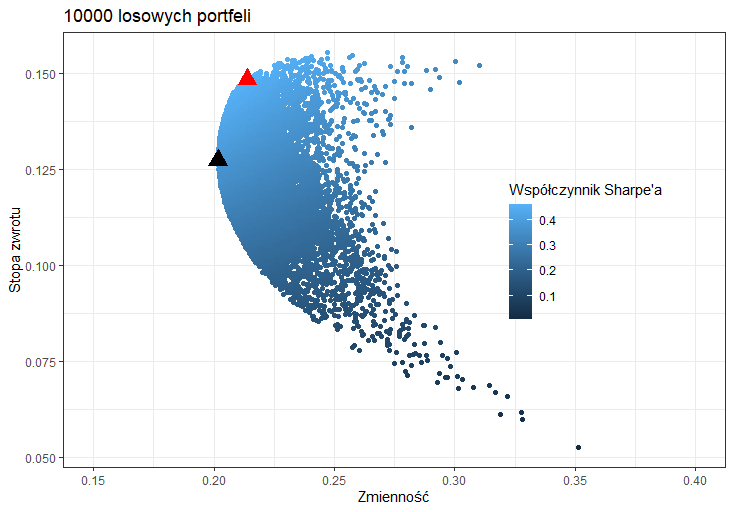
Poniżej widzimy wizualizację wylosowanych portfeli. Czerwonym trójkątem zaznaczono portfel o najwyższym współczynniku Sharpe’a, natomiast czarnym trójkątem zaznaczono portfel o najmniejszej zmienności mierzonej odchyleniem standardowym.

Pełny kod R można znaleźć na Github.
