Modele linearyzowalne

Modele regresji są jednym z podstawowych narzędzi w analizie danych. Zazwyczaj, kiedy mówimy o modelach regresji, myślimy o modelach liniowych, ale nie wszystkie zależności w danych są liniowe. Na szczęście wiele modeli nieliniowych można przekształcić do postaci liniowej.

Modele nieliniowe

Modele nieliniowe to takie, które nie mogą być reprezentowane jako liniowa kombinacja ich parametrów. Przykładowo, model potęgowy ma postać:

$$ y = ax^b $$

gdzie $y$ jest zmienną zależną, $x$ jest zmienną niezależną oraz $a$ i $b$ są parametrami modelu. Ten model jest nieliniowy, ponieważ nie można go przedstawić jako liniowej kombinacji parametrów $a$ i $b$.

Przekształcenie do postaci liniowej

Chociaż model potęgowy jest nieliniowy, można go przekształcić do formy liniowej względem parametrów poprzez zastosowanie logarytmu do obu stron równania:

$$ \log (y) = \log(a) + b \log(x)$$

Teraz, traktując $\log(a)$ jako stałą, mamy model liniowy względem $b$. Podobnie możemy przekształcić wiele innych modeli nieliniowych do formy liniowej, stosując różne przekształcenia do naszych danych.

Przykładowe modele, które mozna sprowadzić do postaci liniowej względem parametrów to:

Model potęgowy dany wzorem $y = ax^b$. Po zlogarytmowaniu obu stron, otrzymujemy: $\ln(y) = \ln(a) + b\ln(x)$.
Model wykładniczy dany wzorem $y = ab^x$. Po zlogarytmowaniu obu stron, otrzymujemy: $\ln(y) = \ln(a) + x\ln(b)$.
Model typu S dany wzorem $\ln(y) = a + \frac{b}{x}$.
Model hiperboliczny dany wzorem $\frac{1}{y} = a + bx$.
Model podwójnie hiperboliczny dany wzorem $\frac{1}{y} = a + \frac{b}{x}$.
Model pierwiastkowy dany wzorem $y = a + b \sqrt{x}$.
Model logarytmiczny dany wzorem $y = a + b \ln(x)$.
Model kwadratowy dany wzorem $y = a + bx^2$.

Implementacja w R Studio

Poniżej definiujemy model liniowy oraz 8 modeli nieliniowych, które można sprowadzić do postaci liniowej.

formulas = list(
  'Linear' = formula('y ~ x')
  ,'Power' = formula('log(y) ~ log(x)')
  ,'Exponential' = formula('log(y) ~ x')
  ,'S-type' = formula('log(y) ~ I(1/x)')
  ,'Hyperbolic' = formula('I(1/y) ~ x')
  ,'Double-hyperbolic' = formula('I(1/y) ~ I(1/x)')
  ,'Root' = formula('y ~ sqrt(x)')
  ,'Log' = formula('y ~ log(x)')
  ,'Squared' = formula('y ~ I(x^2)')
)

formulas = list(

'Linear' = formula('y ~ x')

,'Power' = formula('log(y) ~ log(x)')

,'Exponential' = formula('log(y) ~ x')

,'S-type' = formula('log(y) ~ I(1/x)')

,'Hyperbolic' = formula('I(1/y) ~ x')

,'Double-hyperbolic' = formula('I(1/y) ~ I(1/x)')

,'Root' = formula('y ~ sqrt(x)')

,'Log' = formula('y ~ log(x)')

,'Squared' = formula('y ~ I(x^2)')

)

Następnie dopasowujemy modele za pomocą funkcji lm(), wykorzystując przy tym funkcję purrr:map().

models = map(formulas, ~ lm(.x, data = mtcars %>% mutate(x = disp, y = mpg)))

1	models = map(formulas, ~ lm(.x, data = mtcars %>% mutate(x = disp, y = mpg)))

Diagnostyka modeli

Diagnostyka modeli to ważny etap w analizie regresji. Przy jej pomocy możemy sprawdzić, czy model jest dobrze dopasowany do naszych danych oraz czy spełnia założenia niezbędne dla prawidłowej interpretacji wyników. Przy wykonywaniu testów diagnostycznych przyjmujemy poziom istotności $\alpha = 5\%$.

alpha = 0.05

1	alpha = 0.05

W poniższym fragmencie kodu wykonujemy następujące testy, ponownie korzystając z funkcji purrr:map():

Test t-Studenta na istotność współczynników – hipoteza zerowa (H0) w tym teście to: współczynnik jest równy zero, a hipoteza alternatywna (H1) to: współczynnik jest różny od zera. Odrzucamy H0, jeśli p-value jest mniejsze od wybranego poziomu istotności (na przykład 0,05), co oznacza, że współczynnik jest istotnie różny od zera.
Test Shapiro-Wilka na normalność reszt – hipoteza zerowa (H0) to: reszty mają rozkład normalny, a hipoteza alternatywna (H1) to: reszty nie mają rozkładu normalnego. Odrzucamy H0, jeśli p-value jest mniejsze od wybranego poziomu istotności, co oznacza, że reszty nie mają rozkładu normalnego.
Test Breuscha-Pagana na homoskedastyczność reszt – hipoteza zerowa (H0) to: wariancja reszt jest stała (homoskedastyczność), a hipoteza alternatywna (H1) to: wariancja reszt nie jest stała (heteroscedastyczność). Odrzucamy H0, jeśli p-value jest mniejsze od wybranego poziomu istotności, co oznacza, że mamy dowody na heteroscedastyczność.
Test Durbina-Watsona na niezależność reszt – hipoteza zerowa (H0) to: reszty są niezależne, a hipoteza alternatywna (H1) to: reszty są autokorelowane. Odrzucamy H0, jeśli p-value jest mniejsze od wybranego poziomu istotności, co oznacza, że mamy dowody na autokorelację reszt.

Przez przeprowadzenie tych testów, możemy ocenić, które z naszych modeli są dobrze dopasowane do danych i spełniają założenia modelu liniowego. Model, który spełnia te założenia, daje nam większą pewność, że jego wyniki są wiarygodne i dobrze interpretują strukturę naszych danych. Ponadto w poniższym fragmencie kodu obliczamy również współczynnik determinancji $R^2$, który informuje, jak dobrze nasz model pasuje do danych. Współczynnik $R^2$ mierzy jaki procent wariancji zmiennej zależnej jest wyjaśniany przez zmienną niezależną.

model_tests = list(
  `R Squared` = map_dbl(map(models, summary), 'r.squared')
  ,`Coef significant` = map_lgl(map(models, summary), ~ .x[['coefficients']][2, 4] < alpha)
  ,`Normal residuals` = map_lgl(map(models, 'residuals'), ~ shapiro.test(.x)[['p.value']] > alpha)
  ,`Homoscedastic residuals` = map_lgl(models, ~ bptest(.x)[['p.value']] > alpha)
  ,`Independent residuals` = map_lgl(models, ~ dwtest(.x)[['p.value']] > alpha)
) %>%
  as_tibble() %>%
  mutate(Model = names(formulas), .before = 1)

model_tests = list(

`R Squared` = map_dbl(map(models, summary), 'r.squared')

,`Coef significant` = map_lgl(map(models, summary), ~ .x[['coefficients']][2, 4] < alpha)

,`Normal residuals` = map_lgl(map(models, 'residuals'), ~ shapiro.test(.x)[['p.value']] > alpha)

,`Homoscedastic residuals` = map_lgl(models, ~ bptest(.x)[['p.value']] > alpha)

,`Independent residuals` = map_lgl(models, ~ dwtest(.x)[['p.value']] > alpha)

) %>%

as_tibble() %>%

mutate(Model = names(formulas), .before = 1)

W poniższej tabeli widzimy wynik powyższej analizy. Możemy zauważyć, że:

we wszystkich modelach współczynnik regresji jest istotny statystycznie
tylko dwa modele spełniają założenia dotyczące składnika resztowego – są to model logarytmiczny oraz model typu-S
model potęgowy oraz model logarytmiczny mają najwyższą wartość współczynnika determinancji $R^2$, ale w modelu potęgowym reszty nie są homoskedastyczne.

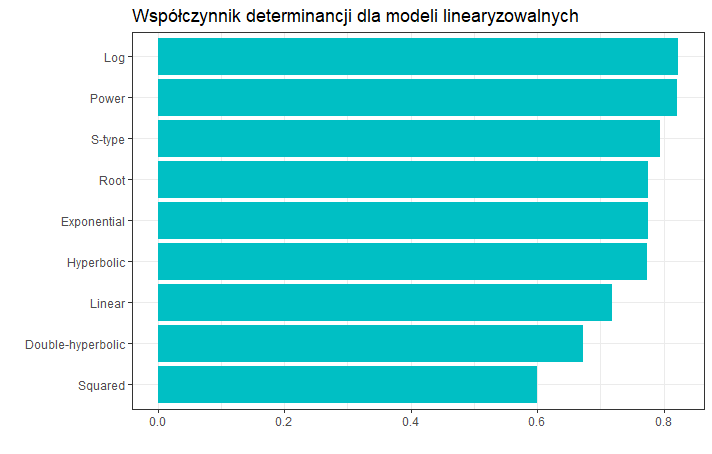
Rodzaj modelu	Współczynnik $R^2$	Parametr $b$ istotny	Reszty normalne	Reszty homoskedastyczne	Brak autokorelacji reszt
Liniowy	0.72	Tak	Nie	Tak	Nie
Potęgowy	0.82	Tak	Tak	Nie	Tak
Wykładniczy	0.78	Tak	Nie	Tak	Nie
Typu-S	0.79	Tak	Tak	Tak	Tak
Hiperboliczny	0.77	Tak	Tak	Nie	Tak
Podwójnie hiperboliczny	0.67	Tak	Nie	Tak	Nie
Pierwiastkowy	0.78	Tak	Nie	Tak	Tak
Logarytmiczny	0.82	Tak	Tak	Tak	Tak
Kwadratowy	0.60	Tak	Nie	Tak	Nie

Na poniższym wykresie widzimy wizualizację wspołczynników determinancji $R^2$ wykonaną za pomocą biblioteki ggplot2.

współczynnik determinancji

Podsumowanie

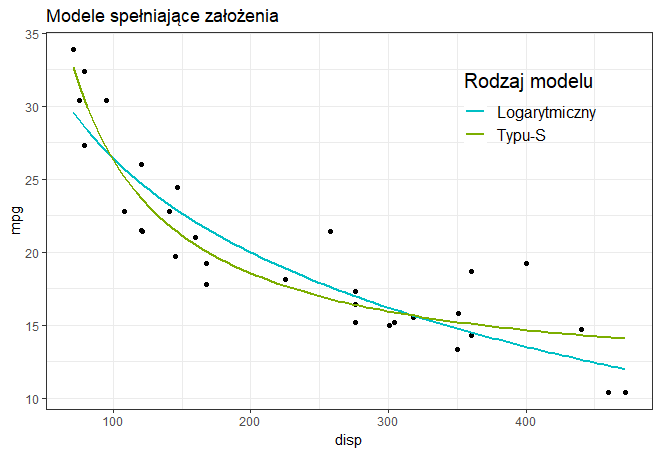
Na poniższym wykresie widzimy dopasowanie modelu logarytmicznego oraz modelu typu-S do danych. Oba modele spełniają założenia dotyczące składnika resztowego, aczkolwiek model logarytmiczny ma większą wartość współczynnika determinancji $R^2$. Możemy zatem powiedzieć, że w tym przypadku model logarytmiczny lepiej pasuje do danych.

modele linearyzowalne